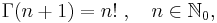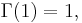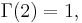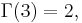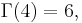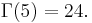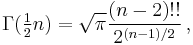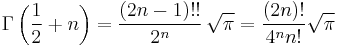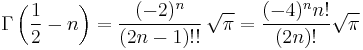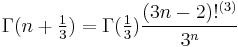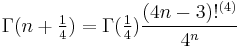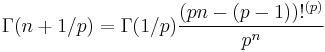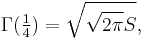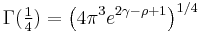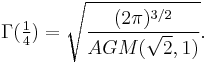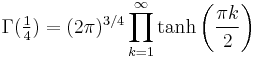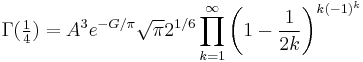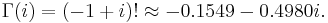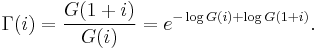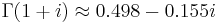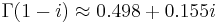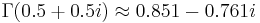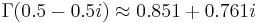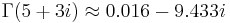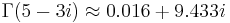Particular values of the Gamma function
The Gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer arguments, but no simple expressions are known for the values at rational points in general. Other fractional arguments can be approximated through efficient infinite products, infinite series, and recurrence relations.
Contents |
Integers and half-integers
For positive integer arguments, the Gamma function coincides with the factorial, that is,
and hence
For non-positive integers, the Gamma function is not defined.
For positive half-integers, the function values are given exactly by
or equivalently, for non-negative integer values of n:
where n!! denotes the double factorial. In particular,
-
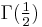
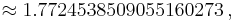
A002161 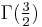
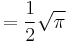
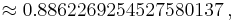
A019704 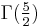
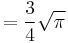
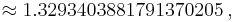
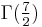
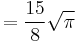
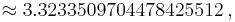
and by means of the reflection formula,
-
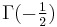
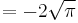
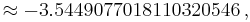
A019707 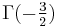
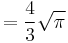
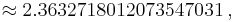
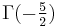
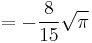
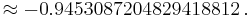
General rational arguments
In analogy with the half-integer formula,
where 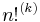 denotes the k:th multifactorial of n. By exploiting such functional relations, the Gamma function of any rational argument
denotes the k:th multifactorial of n. By exploiting such functional relations, the Gamma function of any rational argument 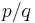 can be expressed in closed algebraic form in terms of
can be expressed in closed algebraic form in terms of 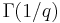 . However, no closed expressions are known for the numbers
. However, no closed expressions are known for the numbers 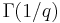 where q > 2. Numerically,
where q > 2. Numerically,
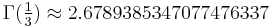 A073005
A073005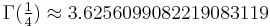 A068466
A068466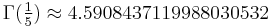 A175380
A175380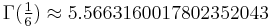 A175379
A175379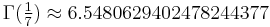
It is unknown whether these constants are transcendental in general, but 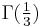 and
and 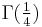 were shown to be transcendental by Chudnovsky.
were shown to be transcendental by Chudnovsky. 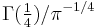 has also long been known to be transcendental, and Yuri Nesterenko proved in 1996 that
has also long been known to be transcendental, and Yuri Nesterenko proved in 1996 that 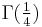 ,
, 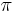 , and
, and 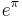 are algebraically independent.
are algebraically independent.
The number 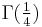 is related to the lemniscate constant S by
is related to the lemniscate constant S by
and it has been conjectured that
where ρ is the Masser-Gramain constant A086058.
Borwein and Zucker have found that 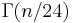 can be expressed algebraically in terms of π,
can be expressed algebraically in terms of π, 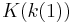 ,
, 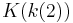 ,
, 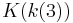 , and
, and 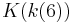 where
where 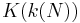 is a complete elliptic integral of the first kind. This permits efficiently approximating the Gamma function of rational arguments to high precision using quadratically convergent arithmetic-geometric mean iterations. No similar relations are known for
is a complete elliptic integral of the first kind. This permits efficiently approximating the Gamma function of rational arguments to high precision using quadratically convergent arithmetic-geometric mean iterations. No similar relations are known for 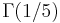 or other denominators.
or other denominators.
In particular, 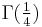 is given by
is given by
Other formulas include the infinite products
and
where A is the Glaisher-Kinkelin constant and G is Catalan's constant.
C. H. Brown derived rapidly converging infinite series for particular values of the gamma function [1].:
![\frac{[\Gamma(\tfrac13)]^6\sqrt{10}}{12\pi^4}=\sum_{k = 0}^{\infty} \frac{(6k)!(-1)^k}{(k!)^{3}(3k)! 3^{k}160^{3k}}](/2012-wikipedia_en_all_nopic_01_2012/I/1d6df4ba904919a7bca1f600d6394713.png)
as well as,
![\frac{[\Gamma(\tfrac14)]^4}{128\pi^3} = \frac{1}{\sqrt{u}} \sum_{k = 0}^{\infty} \frac{(6k)!(2w)^k}{(k!)^{3}(3k)! 6486^{3k}}](/2012-wikipedia_en_all_nopic_01_2012/I/bed1a0ffd90551e82baad0301332c80a.png)
where,
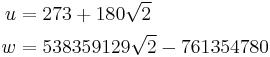
or, since 2w/6486^3 in fact is a cube involving u,
![\frac{[\Gamma(\tfrac14)]^4}{128\pi^3} = \frac{1}{\sqrt{u}} \sum_{k = 0}^{\infty} \frac{(6k)!}{(k!)^{3}(3k)!} \frac{1}{(u\sqrt{2}(1%2B\sqrt{2})^2)^{3k}}](/2012-wikipedia_en_all_nopic_01_2012/I/a9f85aa66b9379a60c82da52f49fa78c.png)
Imaginary unit
The gamma function on the imaginary unit 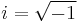 returns
returns
It may also be given in terms of the Barnes G-function:
Complex Arguments
The gamma function with the complex Arguments 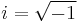 returns
returns
Other constants
The Gamma function has a local minimum on the positive real axis
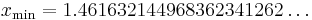 A030169
A030169
with the value
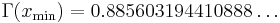 A030171
A030171
Integrating the reciprocal Gamma function along the positive real axis also gives the Fransén-Robinson constant.
On the negative real axis, the first local maxima and minima (zeros of the Digamma function) are:
| x | Γ(x) |
|---|---|
| -0.5040830082644554092582693045 | -3.5446436111550050891219639933 |
| -1.5734984731623904587782860437 | 2.3024072583396801358235820396 |
| -2.6107208684441446500015377157 | -0.8881363584012419200955280294 |
| -3.6352933664369010978391815669 | 0.2451275398343662504382300889 |
| -4.6532377617431424417145981511 | -0.0527796395873194007604835708 |
| -5.6671624415568855358494741745 | 0.0093245944826148505217119238 |
| -6.6784182130734267428298558886 | -0.0013973966089497673013074887 |
| -7.6877883250316260374400988918 | 0.0001818784449094041881014174 |
| -8.6957641638164012664887761608 | -0.0000209252904465266687536973 |
| -9.7026725400018637360844267649 | 0.0000021574161045228505405031 |
See also
References
- ^ Cetin Hakimgolu-Brown : iamned.com math page
- Borwein, J. M.; Zucker, I. J. (1992). "Fast Evaluation of the Gamma Function for Small Rational Fractions Using Complete Elliptic Integrals of the First Kind". IMA J. Numerical Analysis 12 (4): 519–526. MR1186733.
- X. Gourdon & P. Sebah. Introduction to the Gamma Function
- S. Finch. Euler Gamma Function Constants
- Weisstein, Eric W., "Gamma Function" from MathWorld.
- Duke, W.; Imamoglu, Ö. (2006). "Special values of multiple gamma functions". J. Theor. Nombres Bordeaux 18 (1): 113–123. MR2245878. http://www.math.ucla.edu/~wdduke/preprints/special-jntb.pdf.
- Adamchik, V. S. (2005). "Multiple Gamma Function and Its Application to Computation of Series". Ramanujan Journal 9: 271–288. MR2173489. http://www.cs.cmu.edu/~adamchik/articles/rama.pdf.